Cyber: The Maths of Enigma

I'm covering the maths of Engima partially for my own interest, but also to celebrate what the odds were for Alan Turing and his team as today is his birthday, where he would've been 108 today. However, I am going to talk about what he did and why it's incredible that they actually did it.

The Enigma Machine was first invented in 1923 by German engineer Arthur Scherbius as a commercial cipher machine that was in use commercially in the early 1920s.

Before the start of World War Two, Enigma was adopted by the German military as their primary cipher device for encoding messages. From here, multiple different versions of Enigma were created with varying modifications for different branches of the German Army such as the Navy and Air Force.

There were 8 different commercial Enigma devices who were used by the British Government Code and Cypher School to show how these current machines could be broken, to the Italian Navy who adopted these machines for their Navy and during their Civil War.

Then in 1925, a new version of Enigma was put into production and into service in 1926 for the Reichsmarine in a version called Funkschlüssel C, or Radio Cipher C. This was only the first-generation Military Enigma and several more versions came before the infamous Enigma machine that was actively used during World War Two and shown in movies such as The Imitation Game.

In 1934, The Enigma M3 was created and eventually adopted by the US navy. This Enigma machine was superior to any commercial machine as it featured a plugboard to increase the level of security. Another feature of this machine was the ability to swap certain components, such as rotors, to further increase security. The German Army previously used the same three rotors, the German Navy adopted using a set of five rotors, where three were chosen for use and changed nearly every day. As time went on, more rotors were introduced until a pool of eight rotors were available to choose from on any given day.

From here, a newer version of Enigma, named M4, was introduced in 1942 that featured a four-rotor Enigma that was heavily used for U-boat traffic. However, these were not as widely used and so instead I'll be looking at the maths for the M3 Enigma.

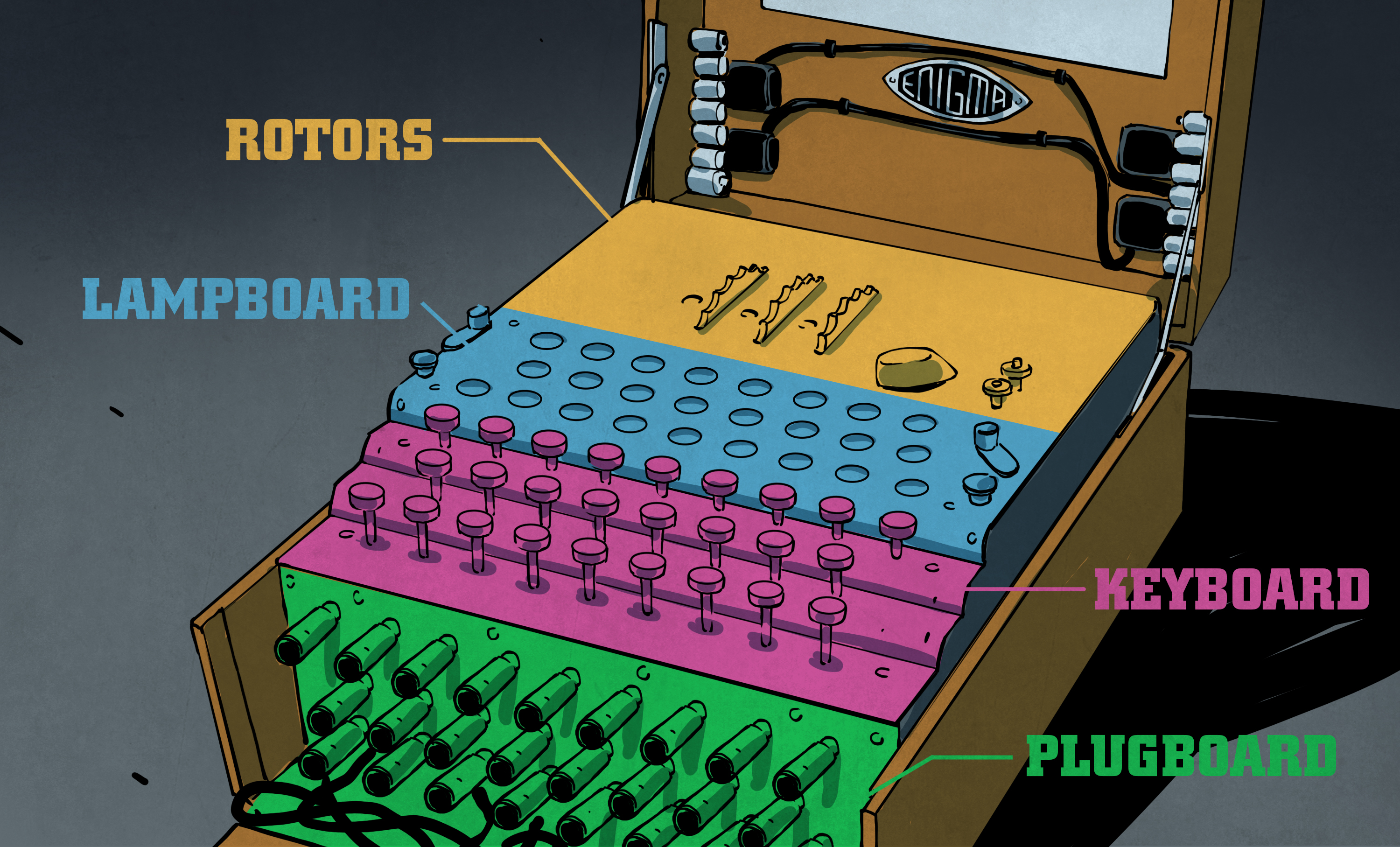
The M3 Enigma, or as I'll just call Enigma from now on, features three major components for encryption. These being the: plugboard; rotors and reflector. Because Enigma is analog, using electrical currents to transmit data and not digital, it is not as easy to understand the possible permutations. However, this can be converted but it is important to understand each element's role in encryption.

Before beginning, it's important to understand what the Substitution Cipher is. If you do not know, Substitution is where you may each letter of the alphabet to a different letter.

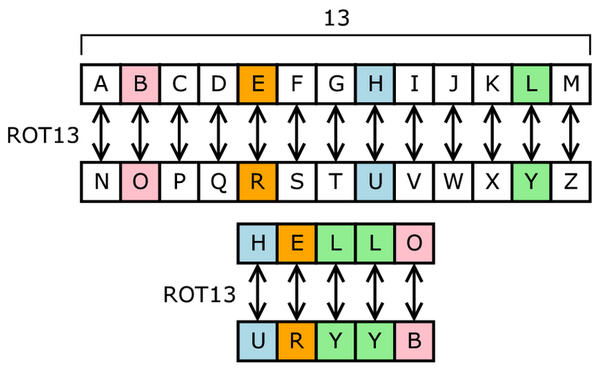
So, if A = C, then typing in an A would give out a C. No letter can be repeated but can be itself. This gives a large array of possible combinations. To be precise, 26! Or approximately 400 septillion possibilities (4 with 26 x 0s). The principals of Enigma revolve around this cipher and allow for the encryption to take place.

Starting with the reflector. The reflector is an item located after the left most gear. The job of the reflector is to receive an electrical current from the rotor, pass the electrical current to a different part of the rotor and feed it back through. It's similar to that of the substitute cipher, however the reflector has a set of pairs so that If you typed in A, you get C. Then if you typed in C, you get A. This is to allow Enigma to be self-reciprocal, allowing the input to be the reverse of the output on a machine with the same settings. This limits the amount of possibilities as it means no input can be itself as the wiring of the reflector has to loop through a different position. This is one of the reasons why code breakers were able to beat Enigma.

Next are the rotors. For the sake of mathematics, we will look at the M3 Army edition where it contained 5 possible rotors. Each rotor had a different set of wiring inside. This wiring performed the same type of substitution but with the added benefit that the connections could move.

After each key press, the right-most rotor would rotate which meant the connections inside would map differently. So, where as A may have equalled B, it now equals E. This was depicted by the rotor's starting position. Each rotor has 26 starting positions, each labelled with a letter of the alphabet. This meant that for just one rotor, there were 26 unique combinations.

However, this Enigma had three rotors, where each could have their own unique starting position. So, we need to find the amount of unique starting positions. To do this, we perform 26 x 26 x 26 = 17,576. However, we have a choice of 5 possible rotors to choose from and only need 3. We can then look at the amount of rotor options. Slot 1 has 5 rotors to choose from, once selected, Slot 2 only has 4 rotors to select from as we can't have two of the same rotors and so forth. Therefore, we do 5 x 4 x 3 = 60. Meaning that there are 60 unique rotor combinations.

Finally, we can combine the amount of unique starting positions with the amount of unique rotor combinations to get the total number of rotor combinations.

60 x 17,576 = 1,054,560 total number of rotor configurations.

This seems like a lot but is in fact relatively small for modern-day computers. The amount of possible permutations for rotors alone is the equivalent of 21-bit key. In modern day computer systems, a bare minimum of a 128-bit key is almost required and a 256-bit key is preferred.

The last element of Enigma is the plugboard. The plugboard is another substitution cipher that can be applied. However, unlike the rotors or reflector, you don't need to have a substitution for every letter. Instead, the Germen Army used on average, 10 connections on the plugboard to form 10 pairs of letters, leaving 6 characters as themselves. This was done for a mathematical reasoning as if you use 13 pairs, the amount of possible configurations decreases. This can be proven via the binomial expansion n!/(n-r)!r!. They proved that when all 13 pairs were made, there were less options than if for example, 10 pairs were made. So, the German Army decided on 10 as a default.

For the amount of permutations, we take the total amount of possibilities being 26!, then we divide these by three separate elements. We divide by 6! Because we make 10 pairs, leaving 6 letters by themselves. We then also divide by 10! Because we create pairs, not individual links so we only create half as many. Finally, we divide by 2^10 due to binomial expansion's law, more specifically relating to the r! division. We do this 10 times so we must divide by 2 to the power of 10 times. When this is all done, we get an output of 150,738,274,937,250. Or more simply: 150 trillion combinations. This is purely based on the plugboard alone.

Finally, combing both the permutations from the rotor configurations and the plugboard means we do 60 x 17,576 x 150,738,274,937,250 = 158,962,555,217,826,360,000. This is roughly 159 quintillion possibilities.

This is an extremely hard to comprehend number, so to simplify, we can convert it back to bits. To convert, we need enough bits to cover this number. The number of bits required to compare an Enigma configuration is a 68-bit key. This is proven via 2^67 and 2^68. We take the higher value because we need to fit the key within the number of bits.

This may not sound like much compared to modern day equivalents of 128-bit basic keys and 256-bit default keys. And you are right. It isn't.

However, this technology is over 80 years old. In 80 years, we have tripled the key size for safe encryption, and we have super computers that can still struggle. Alan Turing and his team at Bletchley park were able to break a 68-bit key using one of the very first computers ever built.

If you enjoyed this post, I'm currently working on a digital version of the Enigma machine that will be available to view and test.

If you have any suggestions or improvements for the blog then please send them to [email protected].