Coding: GitHub Enigma Project

This post is less of an actual blog post but more talking about a new project and outlet. I've now setup a github account where I will be able to post and share projects I've been working on and allow other people to view and download it.

You can check it out here: InJenius on GitHub

This week, I've posted more enigma stuff, but no maths this time. This week is a digital version of the machine that I made using python. As it stands, it's a console application so no GUI, but works the exact same. Specifically, it's an M3 enigma machine that was used during the war and comes with 8 configured gears.

Currently, only 5 of these have been implemented but the rest will be soon. But the actual mathematics behind how it works are the exact same as the original enigma, as well as other online emulators. One extra feature I've added is the ability to either do a single character input like the actual machine, or to type in an entire sentence at once. You can also add new rotors if desired by editing the rotor_details.txt file with new configurations.

I mainly chose to work on this project and in python because I haven't got a lot of experience and I'm looking to gain more. So, I've attempted to use classes and various other pythonic elements and general good coding practice but don't expect perfection right now. I'll be continuously updating the project to include new features, fix bugs and comment the entire code to explain what everything does.

At this point, if you don't enjoy programming then this part probably isn't for you. However, if you're interested in how you turn the physical rotors into a digital system, keep on reading.

The actual mechanics of the rotor function like a substitution cipher. However, the representation of shifts is different. In the rotor, you see that one of the alphabet wheels rotates. This wheel matches with a set of wires and each of these wires is mapped to the other alphabet wheel. When the rotor rotates, it shifts the wiring so that the substitution changes. For computers, you are unable to just move the existing alphabet left or right as that changes the connections, not what they map to. Instead, you need to figure out where the wires point to and find out the amount of shift whether up or down the alphabet.

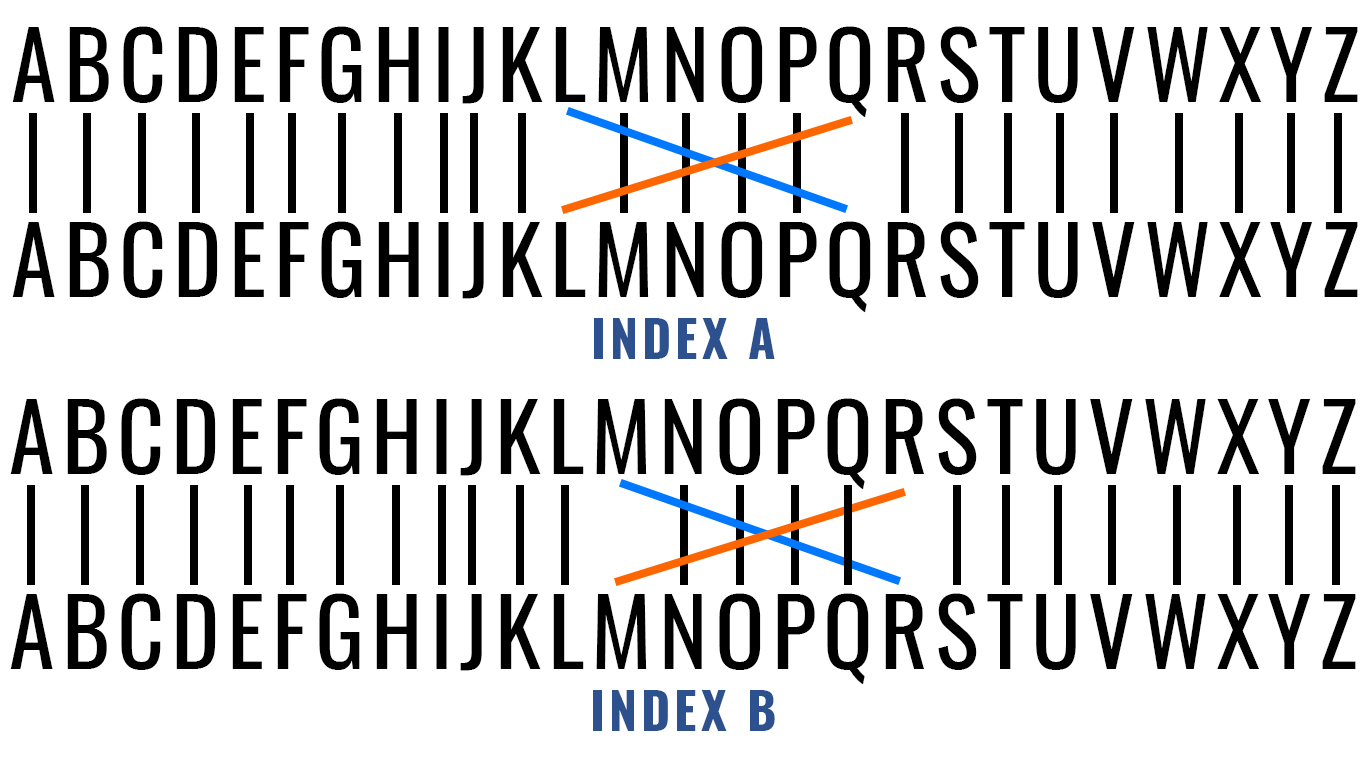
This is a very simplistic view of a rotor with only two unique wires. This is what the substitution looks like when the rotor has an index of A. When the rotor moves to an index of B, it looks like this. Most of these are the same except for the two unique wires. Rather than moving where it starts or ends, the entire connection shifts. meaning that while L = Q, M now equals R. That's where the challenge comes in because you can't just look at what was shifted or the index, you need to know the rotor's current alphabet to figure out the next step. So, after failing several times trying to not make a copy to access later, I eventually set it up so that on each rotor rotation, a reverse alphabet is made so that when queried, the index of the character to encode is used as a key and returns the corresponding letter.

As it currently stands, it's very inefficient as every single character forces all three rotors to create these reverse lookup alphabets, even if it didn't change. This will be tweaked later so that this occurs when updating the rotors for efficiency. However, it's currently functional and the code isn't built for speed in its current state, only as a proof of concept. But this is all available via this link and I'll be updating this project while adding new ones.

If you have any suggestions or improvements for the blog then please send them to [email protected].